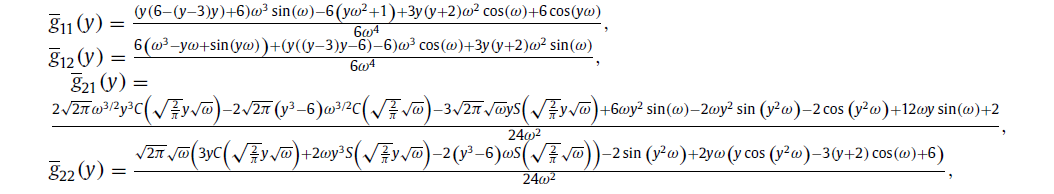
Geng Fazhan, Professor, from the School of Mathematics and Statistics, recently published the paper titled “Reproducing kernel function-based Filon and Levin methods for solving highly oscillatory integral” in the internationally renowned journal “Applied Mathematics and Computation” (The Chinese Academy of Sciences ranking Q1, IF = 3.472) with the first author and Changshu Institute of Technology as the first completion unit. This study developed new Filon and Levin methods for highly oscillatory integrals. The novel method is based on the spline reproducing kernel functions approximation in Sobolev reproducing kernel Hilbert space. The approximation can avoid Runge phenomenon in the setting of high order polynomial interpolation, and there is no restriction on the choice of interpolation nodes. In addition, the form of Sobolev reproducing kernel functions is piecewise polynomials, and the moments in RKF-based Filon method can be computed exactly.

Thesis link: https://www.sciencedirect.com/science/article/abs/pii/S009630032100028X

Paper Title：Reproducing kernel function-based Filon and Levin methods for solving highly oscillatory integral

Journal：Applied Mathematics and Computation

Abstract：

The main theme of this paper is to develop new Filon and Levin methods for highly oscillatory integrals. The novel method is based on the spline reproducing kernel functions approximation in Sobolev reproducing kernel Hilbert space. The accuracy and efficiency of the present method is illustrated through some numerical experiments compared with some effective methods appeared in the literature.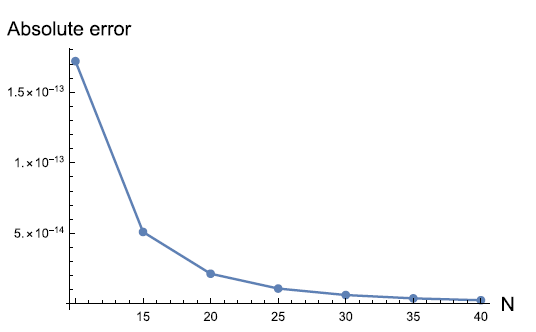  

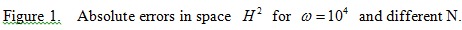
Geng Fazhan is a professor in School of Mathematics and Statistics, Changshu Institute of Technology. He received her PhD degree in 2009 from Harbin Insitute of Technology. His current research interests focus on the numerical analysis of highly oscillatory and singularly perturbed problems. He has published 40+ papers in prestigious international refereed journals.